The McSquared Math Class Blog

This is where you’ll visit once in a while to get certain information, for example, details about a certain activity or assignment. To start out our year, here’s the video-gone-viral introducing the Learn teaching staff!

In the past, I’ve had my students do a memory aid for all of the conics, uploaded to their blogs. This year, you will be making a memory aid, but using geogebra. Since that’s probably more work, I’ve decided that you don’t have to do all the conics – you can make it about the ellipse OR the parabola. I’ve already done the hyperbola for you, so that one’s off the table. But you can use it as a guide so you can get an idea of what I’m looking for.

Your geogebra must include:

• the graph of the conic (see the dark blue and dark green on the hyperbola ggb)
• a display of the rule(s) of the conic, showing the parameters involved in the rule
• sliders for those parameters that change the graph of the conic accordingly
• the values allowed by the sliders should make sense for the conic
• both orientations of the conic (vertical and horizontal)
• for the ellipse: points indicating the foci, the vertices, and their coordinates, segments indicating the major and minor axes, and their lengths
• for the parabolas: points indicating the vertex, the focus, and their coordinates, a line indicating the directrix, and its rule
• a point P that can be moved anywhere on the conic by selecting and dragging it (ie you don’t need a formula for it)
• for the ellipse, the focal radii for the point P, wherever it is, labelled L1 and L2
• the string property displayed as the point P moves around/along the conic (see the light blue and light green on the hyperbola.)
  • show the strings and their lengths
  • for the ellipse show the L1 + L2 property
  • for the parabola show the L1 = L2 property

You will be submitting 5 identity proofs. You have SOME choice about which ones though!

Your 5 must come from the examples indicated in the grid below, all of which come from Visions 2 and Carousel 2. Your mark depends not only on the correctness of your proof, but on the level of difficulty of the examples you choose. For example, if you choose 5 hard ones, and you do them all perfectly (see below for what I mean by “perfectly”), then you’ll get 100%. If you do 5 medium ones perfectly, you’ll get 85%. Note that there are only 4 easy ones, so nobody can just do all easy ones. Oh yeah, that’s right, I’m way ahead of you.

So…what do I mean by perfect?

• Correct procedure:
  • one side is simplified at a time
  • each line shows one step only
  • each line is justified with a trig identity or an algebraic procedure
  • QED, baby!
• Correct math, of course

Also note that if you do MORE than 5, I’ll mark the best 5. You should also know that there are some here that I actually have not been able to figure out how to prove. YAY! Maybe one of you will put me out of my misery!

In epearl: (10 marks)

• Task description (of blog post only)
• List of criteria (for blog post only)
• At least two drafts for your blog post. (I’m not talking about drafts of the complete blog post. I mean two things that contain info/text that eventually morphed into your final blog post. An outline, or a first attempt at explaining your calculations…..)
• At least two versions of your geogebra/desmos.
• A reflection for each draft, and a reflection for each version of your graph. Make sure it’s clear to me which reflection goes with which, eg label with “reflection for draft 1”, or “reflection for version 2” for example.
• All of these entries should not have the same date stamp on them. Know what I mean?

In your blog post: (10 marks)

• A working geogebra/desmos, for the height and the distance. The graph should be either linked from your post or embedded directly into it. (Sakai-message me the embed code like usual, but tell me where you want it embedded in your post. I don’t want to mess up your visual impact!)
• Connections: For any one of your rules (as long as it has an h ≠ 0 in it): The connections between each of the four parameters and some concrete physical part of the VFW or how it behaves. Explain your reasoning.
• Validation: Show me your validations for:
  • each rule – how have you checked to make sure that it actually represents the height of the VFW car on the VFW?
  • your graphs – how have you checked to make sure that they actually match the graphs that you did way back on Feb 25?
  • your equivalent rules – how have you checked to make sure that they are actually equivalent?
• Proper notation and use of symbols in wordpress editor (click on “show kitchen sink”)
• The last thing: One reflection from your epearl, or a new one, that sums up what you learned in doing this assignment. 2-3 sentences. Anything you want to say, just make it honest!

In your graphs: (5 marks)

• Big easy-to-spot labels for each graph: What the graph represents & the units of measure for the axes
• Two equivalent rules for each function
• They should be correct too!

Bonus points:

• Enhancements in your geogebra/desmos, eg animation, colour coding, check boxes, sliders, anything over and above the list, as long as it enhances the math information somehow
• Any other type of media embedded in your post to enhance your explanation, ie pictures, video, codecogs etc
• A rule about the height of a car on an actual ferris wheel that really exists. There are some pretty big ones!
• Tweet a link to someone else’s blog post to some other Learn person

Due date: Friday, March 28. More details to come about what I’ll be looking for, possible bonus points, how it will be assessed etc, but I thought you might like to start thinking about this in the meantime:

The blog post

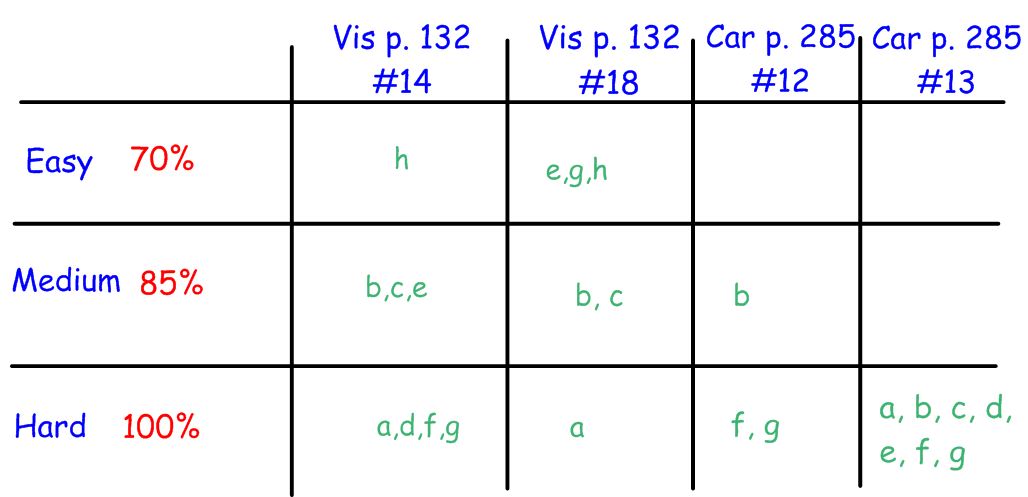
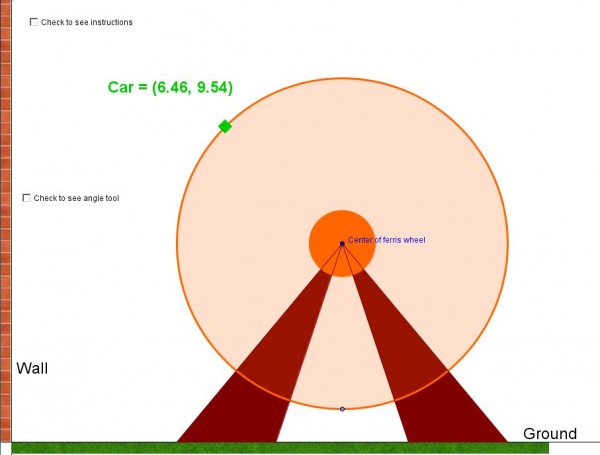
This blog post will be about the VFW, from week 24, the one for which you already created graphs, before you knew anything about trig functions. Remember these?

Your job now is to get these same graphs to appear by figuring out their rules and typing them into either Desmos OR Geogebra. Your post should include:

• Explanations for how you arrived at the rules, including each of the parameters.
• An explanation for what each parameter represents on the ferris wheel (ie radius, speed, etc)
• A desmos OR a geogebra that validates your rules (can be embedded or a link, but it has to be functioning, not a static snapshot). The x axis must be in seconds, not degrees or radians.
• Each of your rules must be accompanied by a second alternative but equivalent rule.

The Story Behind the Blog post

You’ll be doing this part first! You will develop and polish your blog post in epearl.

• Just like when you did the geogebra assignments, you will upload the various versions of your graphs as well as your blog posts. You may type your drafts directly into the epearl text editor, or do the posts in Word and attach each version of the Word document.
• This time I will assume that the final versions are the ones that appear on your blog.
• Your artifact must include a task description, criterion list, and at least 2 versions of the graph-post, each version accompanied by reflections. This is so that I can give you feedback as you work, and also so that you can learn not only about trigonometry, but also about learning.

Some suggestions for your reflections:

• Reflections on this assignment:
  • Any incredible insights you had while doing this assignment, and what brought them about, a conversation, a good night’s sleep…
  • Anything that you found easy, and why you think it was easy
  • Anything you found difficult, and why you think it was difficult
  • What you did to try overcome any difficulties
  • Any connections you notice to something else we studied this year, anything at all that you were reminded of, and why
  • Your thoughts on the impact of doing these graphs first without any trig knowledge, then reproducing them with the theoretical background – help, hindrance, or meh?
• Reflections about your progress:
  • A direct quote from an earlier epearl reflection that shows you’ve progressed since then (or regressed, but hopefully not)
  • A successful strategy you used before that worked again on this assignment
  • Your thoughts on Desmos compared to Geogebra – which one, if any, has helped you in your comprehension, and how?

Here are some examples, from my own blog, of your reflections on past assignments, all good, all the kind of thing that’s worth writing down: example 1, example 2.

Just so you know, I don’t ask you to do anything I don’t do myself, so for an example of learning accompanied by self-reflection, I invite you again to read a post I did on my own blog about logs. Self-reflective AND full of selfies too!

Today’s padlet wall is brought to you by St. Patrick’s Day!

Created with Padlet

Now that you’ve played with Desmos a bit, we’ll use it to investigate TBS more closely. Here’s what you’ll be doing:

1. Go to the desmos site , and type in the equation of the unit circle: x² + y² = 1. You might want to zoom in a bit so it’s not tiny,
2. Type in the equations of the coloured lines that correspond to the big seventeen, ie these lines:
3. Trim the lines so that they don’t extend beyond the unit circle. You’ll have to tell desmos the domain or range of each line to do this. For example, for the red line y = 0, you must specify a domain of [-1, 1]. In desmos, you do this by typing, next to the equation, {-1 ≤ x ≤ 1}.

Once you’ve done all you can, upload a link to it here, with your name as the title.

First of all, hey there! I hope I have as many students now as I had on Feb 28! I look forward to hearing about your adventures.

I started my March break by blogging about logs. NO NERD JOKES! So if you’re interested in why the log rule can be simplified to only two parameters, you can find out in this post from my own blog: “The Day My Brain talked to Me, or How I Learned to Think like a Logarithm”  It’s also highly amusing, so even if you’re not particularly interested in hearing more about logarithms, you might still like it.

Today’s menu:

1. In class: Recap of everything we’ve done in trig so far, using google drive.
2. In class: Something new called radians. In Zen.
3. After class: A voicethread about radians.

Everything’s at sakai – I’d put the links here but different people have different links, so…I’m too lazy to re-do it all.

After we discuss yesterday’s graphs, you’re going to do pretty much the same thing, except this time, on an impossible Ferris wheel. You’ll see why it’s impossible when you open the geogebra.

Once again, you can print up these notes in case of bor mishaps, which there were some yesterday. But I really hope to see more graphs today!

You’ll be moving the little car around and recording its height at various angles, then graphing the results and sharing them on this padlet wall for the height.

Then do the same for its distance from the wall. The padlet wall wall is here.

You probably think you already know what the graphs are going to look like, don’t you? 😉

Big day today! Everything you’ll need is here, files, instructions, etc, but I have also put copies of everything in sakai as well, just in case things go awry from here.

First, download and print a copy of this, just in case we have problems in the bors today:

Student tables and graphs by amcsquared

Next, get this geogebra open and at the ready.

In it, you’ll find a virtual ferris wheel, on which you can move the little green car around. As you do, you’ll notice the ordered pair that follows it:

The instructions are all right there in the ggb, but basically you’ll be making two graphs about this green car, one about how high it is above the grass at various times, and the other about how far from the brick wall it is at various times. If our bors work well, you’ll be doing those graphs there, if not, you’ll be doing them on the printouts.

Once those graphs are done, you’ll be uploading a shot of them to the padlet walls below.

This is not for marks, this is for full-on learning, so relax, focus, and have fun! Although fun is not how I would describe my last time on a ferris wheel:

Here’s the link to the padlet wall for the height graphs:

Created with Padlet

Here’s the link to the padlet wall for the distance graphs:

Created with Padlet

What a lovely sight – a word cloud generated by the Learn Students! Thank you all so much! I’ll let my Valentine’s day friend say it for me: