The McSquared Math Class Blog

Here’s a quick video on how to program the quadratic formula into your TI calculator. Sorry, I didn’t have time to add my actual voice to it:

Where L1=L2 the point is part of a parabola.

The parabola is the locus of a point that the same distance from a fixed point and a line.

theLocus definition of this graph is that since the locus is the path fallowed and it is in a perabolic shape due to the position of the line and the focus when L1=L2

Li=L2

the locus deinition for a porabola is every point on the porabola will make a have a L1 and l2 of the same lenght l1 is formed from the focus and the l2 is formed from the directrix

all point on the parobola both l1 and l2 are the same.

L1, which is the line between A point and the Focus + L2, which is the line between the same point and the directix = the same length. All the points in which they equal eachother forms a parabola 🙂

The locus definition of a parabola is when Li is equal to L2 when choosing one point on the parabola

a line, made up of points which are equidistant from a fixed point and a fixed line.

I will be using a kind of a checklist to evaluate your conics memory aids. I’ll be looking for any 15 things from the list. As such, your mark will be out of 15, but the list has 20 things on it. Yes, it will be possible to get more than 100%! And, there is more than one way to arrive at a perfect mark.

Here’s the list:

1. The basic info:
   1. all 4 conics
   2. their locus definitions
   3. their graphs, in all their possible orientations
   4. the rules that correspond to the conics/graphs
   5. the parameters for each conic: where they are in the rule, where they are in the graph
   6. all the parts of the conics, names, definitions, locations
   7. any and all formulas pertaining to parts
   8. any and all properties of the conic
2. Organization:
   1. information presented in an orderly, logical, easy-to-follow way
   2. visual information as well as textual info, AND correspondence between them
   3. colour coding that makes it easy to see the organization – ie the parameter a is always coloured red in text and graph, or all your ellipse info is turquoise….
3. Depth:
   1. the information is organized in your own order, so that I can see you didn’t just copy down all the notes I gave you
   2. comparisons between conics
   3. something new – something you noticed but that I never said
4. Rigour:
   1. worked-out examples, like finding the rule given certain info, or solving your own problem involving conics
   2. actual concrete drawings of conics done with string(s) (hey, you could video yourself like I did! But no walls.) (I’m serious, put the pen down.)
   3. alternate forms of the rule
   4. inequations involving conics
5. Extra:
   1. any use of tech that enhances the message (codecogs, geogebra demos, a voicethread, embedding using scribd……)
   2. publishing on blog without handwriting

So as you can see, if you just do the basic info, and it’s all there, and it’s all correct of course, you already have 8/15, which is almost a 60%. If you want to pass, just add one more thing. If you want to get 100%, well, you can do the math. Lol! Get it?

Here are a few concept maps from previous students:

http://www.math-joey.blogspot.ca/2012/03/my-independent-assignment-session-6.html

http://kkailyg.blogspot.ca/2012/04/ia-concept-map.html

https://patrobic.wordpress.com/2012/03/24/fractals-independent-assignment-the-most-complete-outline-ever/

http://prezi.com/explore/search/?search=Step+Dancing+and+Math#search=Step+Dancing+and+Math&reusable=false&page=1

For this one look at the second post to see the concept map: http://kiddmath.blogspot.ca/

https://docs.google.com/presentation/d/12WUUja1icO6uSz1muxJOz1d6VLwA-W5K1ZYf6t6AoJM/present#slide=id.p

http://katsbrainseepage.blogspot.ca/2012/03/more-then-one-infinity-o0.html

Your assignment is to do any three of the identity proofs  from Visions 2,  p. 132-5, nbrs 11, 14, 18. All are not the same difficulty, however, so they’re not all worth the same mark. Here’s a table to tell you what each of those questions is worth, if done perfectly: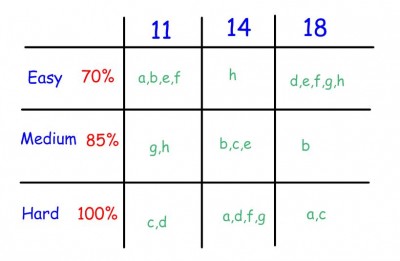

Now here’s what I mean by “done perfectly”:

• Uploaded to your blog
• Every single step is shown
• Every single step uses proper notation (ie not just “cos”, but “cos x”, and none of this “cos^2x” nastiness – I want to see cos²x!)
• Every single step is explained by identifying the type of identity used and/or the algebra
• The overall form is correct (LHS seperate from RHS, both sides =, QED)
• It is all correct.

So if you do three easy ones perfectly, you’ll get 70% on this assignment. If you do one easy, one medium, and one hard perfectly, you’ll get the same mark as if you did three mediums perfectly.

Here’s an example of one done perfectly (if I do say so myself) in handwriting:

As usual, bonus points are rampant! Use codecogs, paint, Microsoft Equation (that comes with Word/Powerpoint), Mathtype….bring it!

Just like for the last post, you have to be up to date on all your regular blog posts in order to qualify to do this instead of the in-class test. This means all of the following must be done, and done well:

• solving trig equations 1
• solving trig equations 2
• the six ratios
• freaky functions
• reciprocal, quotient, and pythagorean identities

The blogpost:

Part 1:

Solve any two of the problems posted at SAKAI. Show all your work, including your rule, the graph that represents the situation, and all the steps in your reasoning. Don’t forget to validate everything.

What I’ll be looking for:

• all work shown
• work well organized and easy to follow your reasoning
• proper vocabulary and notation
• a graph to accompany your work
• validation of your graph and your solution

Part 2:

Do Math 3000 p. 245 nbrs 9, 10, 11. Please show every single step of your simplification process, and explain what you are doing in that step. For example, if you are replacing something using an identity, indicate what you are replacing with what, and which identity you’re using. If you are doing an algebraic simplification, explain exactly what you’re doing. Do not use the abbreviations I used in the voicethread for your blog post!

• All steps shown and explained as above
• proper vocabulary and notation

Bonus points available in both sections for anything extra, like exceptionally cool graphics, or use of a web tool to embed something into your post (eg codecogs, scribd, vimeo), or just plain personality and pizazz!

This happens since the angle cannot reach the asymptote yet it can be veeerryyy close to it! There are so many asymptotes because of the amount of lines the function has! 🙂

because there is a vertical asyymptote

Because as x gets closer to 90 degrees the value of y increases very quickly forming almost a straight line, there are so many asymptotes because every time x has a cos of 0, meaning at 90 degrees, 270, etc… there is an asymptote

when tan gets really close to 90 degrees it explodes, the tan cants get to 90 degrees, actually every 90 degrees is its asymptote because the function cant attain it

because 90 degrees is one of its asymtote antherefore it increases dramatically because it cannot touch 90 degrees. there are so many asymtotes because the graph is made of many lines that never connect, these lines are seperated by asymtotes, therefore many asymtotes.

Tan does look confusing and is exceptionally different than the rest of the ratios as to how it looks on the graph. the properties are one thing that I need to be working on, although they are not that difficult, it takes me a little whole to find all properties, I need to practice it finding them quicker

I think that the tan function goes vertical when approaching 90 degrees because it will always get and closer to the asymptote, but it will never actually reach it. It increases its y-coordinates very fast as the x coordinates increase very slowly, in fact by only one decimal. I think that there are many asymptotes because if we follow the unit circle, the basic tangent function follows the quandrantal angles in a period of 2pi.

Check Cass’s post on this, checklist entries are here:

On the right triangle, tan is leg1/leg2 , on the unit circle tan is sin/cos

tan is sin /cos =P

Tan on unit circle: the tan of any angle is always the sin of that same angle/cos of that same angle.
Tan on right triangle: Sin Data/ Cos data

On the unit circle, tan is the ratio siinx/cosx. It follows the soh cah toa fashion, which doesnt make too much of a drastic change for us beginning to learn tthis.

I have no idea.. I’m trying to figure out how it works because I really don’t for now. I’ll discuss with classmates when I’ll have the opportunity.

Trig equations 1 (no b or h involved): you can see some directly from blogs, like Cass’s post  and Tanyse’s post and here are those that came in via the checklists:

Firstly, we must make equation equal to zero since we are looking for the x’s which are the zeroes! After simplifying the equation algebraically (if needed), we work our memory into remembering which of The Big Seventeen is equal to either the cos or sin of an angle. After doing so, we write down our findings and make sure to include that all their coterminal angles are also part of the answer! 🙂

well i would start off with having remembering that cos =x sin=y when dealing with ordered pairs so if u know all the order pairs u can easily solve em. also all the b17 in radians. also there can be to possible answers!
well that it d(^-^)b

do the algerbra isolate cos or sin x
look at big 17 and find the cos(x) or sin(y) values that match with value found (could be 2)
add all cotermial angles +-2pin,n=N (plug n with a number to slove for a cotermial angle
and there we go

first you have to find the angle in radians, there can be more than one angle and if there is you have to use them all. Next you have to add it to 2pi and you get a coterminal number. THen you have to times the next whole number to 2pi and continue or you can just add the mulitple it increased by to make you life easyer

I solve them by isolation the x. The I find the angle that corresponds to an angle on the unit circle. Then I add 2 pi n.
How will we know if there is a solution or not? How do we know if there is one of to values for the same point?

This you have to find what angles have the same y or x values. There can be more than one. Then you look for the coterminal values

How to solve them: When looking at the equation, we must first start with the number that has a positive or negative sign, we put it on the opposite side. Then we being the number where there it is multiplying on the other side and then we get an a fraction.

I isolated the x of cos or sin then found the coordonants then + 2 pi n

When you have the equation, frst step is to isolate the cosx or sinx. Then you need to remember the trig point on the big17 that goes with it. The siin(y) and cosss(x) trick are very useful.
My question is, how are we going to solve the equation when its not a point we learned on the big17?

The way to solve them is isolate the cos or the sin and the x. Then find the point on the unit circle and find the value for that point

Depending on what is given, sometimes you only have to look at the ‘Big Seventeen’ chart and you have your answer right away. But when it gets more difficult, the most important aspect is that you make sure to analyze the formula/equation given as closely as possible.

First you need to iscolate the sin(X). so depending on what variables are in the equasion, have to use different options to do so. once you have sin x = .. lets say 1. we convert it to radians. at what point is the height 1? at pi/2 radians. that is our answer, and this is a zero of the function. to represent all the other zeroes of this function as well, we write “+/- 2piN” because the Zeros reoccur every 2 pi. if there is an h, we have to add it to the 2pi, because the cycle wouldnt be reoccuring at every 2 pi any more. My question is : are we goin goin g to use this method to solve for other y values in the function. But i guess it is probably quite obvious that that is what we are going to do.

1. algebra (isolate cosx or sinx)
2. Remember or check reference (to find which angle fits with the result of coordinate x or y)
3. write the angle(s) and their coterminals (or the formula which means the coterminals )
XE( x= angle in radians + 2 pi n, or x = other angle (if there is one) in radians + 2 pi n, XE N (whole numbers))

In case anyone needs to see what those graph should look like after you type your rule into geogebra, here they are. I know they’re fuzzy, best I could do!