The McSquared Math Class Blog

First of all, the due date for this post is March 22, which happens to be the date for the test. Coincidence? NOT! Anyone who seriously plans to do this should get cracking!

Your post must have two parts to it:

Part 1:

• Design your own ferris wheel, specifying its size, location of centre (relative to a wall and the ground), rotation speed, exactly where people get on, & how many spins each customer gets. Note that all of those values must be different from those that were used in our ferris wheel in class.
• Show the graph for either distance from wall, or height above ground, as a function of time, for their entire ride.  Give 2 different rules (one using sin and the other using cos) that could represent your graph.

What I’ll be looking for, apart from the above:

• proper vocabulary and notation
• a complete description of your ferris wheel, in English, including which quantity you are depicting on the graph (distance from wall or height – don’t make me guess which one)
• a ferris wheel that could conceivably exist (ie it doesn’t go underground or behind walls)
• a graph that fits that description, with clearly labelled axes
• two rules that both fit your graph
• validation of your graph and your rules

Part 2:

Solve a problem by modeling it as a trig function:

• Pick any of the 4 problems posted at sakai
• Include in your work, the rule for the situation, with defined variables
• Include a graph representing the situation, with all axes labelled
• Include your solution to the questions

What I’ll be looking for, apart from the above:

• all steps shown and explained
• well-organized work that is easy to follow
• validation of your rule, your graph, and your solutions
• correct rule, graph, and solutions

Bonus points available in both sections for anything extra, like exceptionally cool graphics, or use of a web tool to embed something into your post (eg codecogs, scribd, vimeo), or just plain personality and pizazz!

Hello out there, ferris wheelers! I went through all your blog posts this week and pulled some snippets that really stood out to me, for many different reasons, but the one they all have in common besides general awesomeness is this:

They contain words that I never said.

The words, and therefore the thoughts, belong to you, they came from your brains, which means you stretched your brains beyond what happened during class, or a voicethread, or while you’re doing homework examples, or while you’re doing a test. That’s real learning, folks, it’s not about what I do or say, believe me.

And then you shared these thoughts with THE WORLD. Everybody wins!

Well done, all! Here are the snippets so far, as of this moment, which is Sunday lunchtime, but if more pop up between now and tomorrow, I’ll add them too:

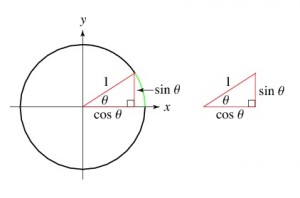
On the unit circle:

Lizzie, a truly neat formula for coterminal angles:

You can have different numbers for the angles by using a single “initial” angle. The most common angle would be : 90 degrees. So let’s say 90 degrees is your “initial angle”, it’s ‘synonyms’ can also be; 450 , 810 , 1170, even – 270 and -630 degrees. A mathematical rule for this example would be : 360 x + 90 = y     where y= resulting degrees and x = full circle counter-clock .

Tyson, on finding a coterminal angle for a negative angle:

When an angle given to you is negative, don’t let it confuse you, the same process is used to find coterminal angles (adding 360).

On the Big 17:

Amanda, on how she remembers the radian angles by their denominators:

Basically, I separate the circle into sections; the “over” 1s, 2s, 3s, 4s and 6s. Then, in my mind I visualize the lines that would be there and place my values.

Jessica, using a visual relationship to remember the radian angles (and not the one we talked about in class, either):

I have worked on the ferris wheel with Javiera and we have both realized that there is a mirror image ( for the denominators)  from left to right. also we have realized that the fractions that are the same color all around the circle, have the same denominator

Cassandra, another memory aid for radians:

My tip is that the first is a red cross which represents the quadrantal angles. Then we separate this cross into 4 pieces with yellow lines. Then we split the 180 degrees into 3 with pink lines. And finally we separate the 6 angles into halves with green lines.

Duncan, on remembering via UNDERSTANDING:

I think the easiest way to remember radians is simply to remember that 180 degrees is equal to pi radians. From there you can divey it up with fractions and the likes, 30 degrees equals pi/6, 90 degrees equals pi/2, 120 degrees equals 3pi/4, so on so forth.

David, a comment about commenting, which is the lifeblood of blogging, in my opinion:

(i saw and liked Amanda’s way that was the only post i saw so id love to know your tricks) or maybe you just have photographic memory which would be awesome.

David again, made me laugh in a comment on Marianne’s post:

My favorite part of your post is all of it and i also enjoy reading you other post you keep it orgainized short and simple which is wonderful….i also really like how you put the images big so we dont have to click on them we can see them within the blog post unlike mine ahaha

On the 2 basic functions:

Marianne: pictures that are worth 2pi-thousand words:

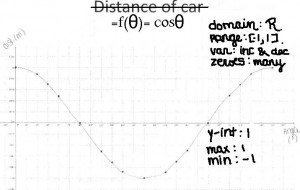
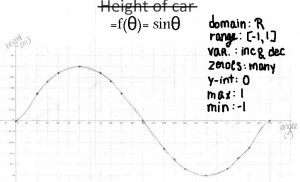
Justine, noticing something that will be SO important very soon:

Both graphs look like a wave  Only the “height” one looks shifted to the left compared with the “distance from the wall” one.

Cassandra, also making me laugh, and I am so calling them this from now on:

Well today we learned the actual function to this cool wavy function that I call the “ferris wheel function” since I find “trig function” is boring. So we actually learned how to see SIN and COS in a different way.

Fred, with a great way to visually and conceptually link the ferris wheel to the functions:

…we have learned that if the wall is on the y axis and the ground on the x axis. both graphs will look exactly the same except that they won’t start at the same place.

Mason, with handy calculator tips:

Today in class we discovered that the rules for the 2 Ferris wheel graphs are y=cos(X) and y=sin(X) and how to graph it on your calculator; Which I will NEVER remember, but while I do, I’ll share it! LOL  1) Select Y= 2) Eneter in Y= sin (x) 3)press ZOOM 4) Choose Ztrig 5) Press Enter and Watch the line!

Tanyse, with a short but powerful summary of the big picture:

we worked on pulling information from our unit circles to form a table and then use that to graph……

Javiera, on what the basic functions have to do with the unit circle ferris wheel car:

So when we are making a graph for sin we are really graphing the distance from the floor according to time….when we are graphic cos we are really graphing the distance to the wall according to time

Javiera again, just an awesomely insightful and deep thought about why we made two graphs from the single ferris wheel (I seriously got goosebumps when I read this):

I think we do this because we have 3 variables going at the same time: The height, the distance to the wall and the time and since we only do 2 variables at the time we separate them into two different graphs and of course the time is the x since it is the independent variable

Elise, on the connection between trigonometry last year and this year:

I now understand where the trigonometry comes into account in the function.

David: on how to remember which function is which ( okay I did say this, but I like the emphasized spelling:

sIIIInn  yIIIIII    heIIIIIIght

coSSSS  xSSSSS   diSSSStanCCe

Tyson. the psychic student, thinking ahead to when we’re dealing with circles other than the unit circle, which, by the way, you actually already have:

To my knowledge, this method only works if the circle has a radius of 1 unit, so my guess is that if the circles radius is bigger than that, we will have to add that into the equation somehow.

On special properties of trig functions:

Cassandra, on how to recognize a cycle, and how to recognize a NON-cycle:

To remember: all cycle have the same width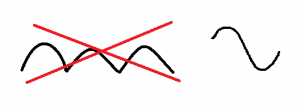

Eli, adding an important detail to my definition of frequency, which believe me will be there from now on:

The frequency-is equal to how many cycles there are up to 2pi= a full circle

Jack, using his own vocabulary which is all kinds of awesome:

…l.o.o or as i like to call it the equilibrium…..a cycle is a part of the curve that if you would put next to similar part it would make a wave. a period is the distance from one crest or trough to another….the amplitude is the distance between the crest or trough to the equilibrium.

Tyson, on frequency:

The way that I remember what the frequency is, is by looking at the word. Frequent means often, so frequency is how often something is happening within an x value of a graph

And my final words.…now that you have all done such amazing work, you do realize what this means, don’t you?

We are so going to keep doing this, folks. But tell me what you think, especially those of you who actually posted every day, do you think you understand this stuff better as a result? What about reading other peoples’ thoughts, either here or on their own blogs?

Here’s the animation I showed in today’s class. Here’s an idea for anyone who wants to NOT do a trig test:

Create a geogebra that does one of these types of animations! How? I have no idea, I’ve never done any kind of animation with geogebra. All I know about geogebra I have learned by playing around, and watching the odd tutorial at the geogebra.org site.

But I can tell you this, if you figure it out and get it to work, there is no way you need to do a test to show me what you know about trig, because such a geogebra would be enough!

Well that’s a bit better! More great posts from Cassandra, Marianne, Justine, and Javiera, and also Elise, Mason, Lizzie, Jack, David, Amanda, Jessica, Eli, and Michael have added their’s. Now it’s time to start commenting on other peoples’ posts – whichever one(s) you feel is the best summary, or has the best picture, or whatever! Your comment should start with something like “My favourite part of this post is…..”

And just for fun, here’s a game you can play that proves we humans have math in our genes, or at least in our eyeballs! It takes a few minutes, you get three tries, and they give you your score after you’re done. Mine was 6. Beat that! Actually, you probably will.

Everyone is supposed to have done their first blog post as of now, but only 4 people have. My sincere appreciation to Cassandra, Marianne, Justine, and Javiera! A reminder to everyone else – not doing these posts means you’ll miss out on three things:

1. The chance to improve your learning along the way and hence gain a deeper understanding.
2. The chance to demonstrate your understanding to me and get help along the way, instead of when it’s too late.
3. The chance to not write a test on trigonometry.

Get cracking! It doesn’t count if you leave it all to the end people!

Many thanks to our awesome principal Dianne Conrod for teaching us how to skate like this!

Musical flowers that Duncan made for a certain special lady in his life for Valentine’s Day – a very lucky girl!

I had wanted to make a video of this, and I will still try to, but here’s this for now to get you started:

Simple Programming for the TI calculator by amcsquared

Some of you weren’t there when we did this in class, and apparently the archive doesn’t show all the slide images, so here are the slides I showed of peoples’ log explanations from  last week:
You might have to click on the image in order to be able to actually read it. If your’s is missing, it must have appeared too late for press time!

I have been getting a lot of positive feedback from some of you about having you write your thoughts on the checklist instead of the blog. Some say they prefer it because of the relative anonymity it gives you, and this frees you to speak your mind. But some people prefer it because it’s just one less place to go, one less click, etc to complete.  In either case, I encourage you to use those blogs as much as possible, not only because it means there will be one less thing for ME to do (ie copy/past/post it here) but because you need to let go of the idea that you are the only one who is:

1. having issues
2. not having issues
3. shy
4. not feeling the love for logs
5. totally feeling the love for logs
6. having a strange desire to write a poem about logs and blogs because you noticed a while ago that they rhyme
7. whatever!

I also want to point out that SOME people have been using their blogs for a variety of things, posting gorgeous assignments, reflecting about math, reflecting about other stuff, and you should check them out, and leave them a comment. A good comment, for example, “I like this part of your post because…..” or “I don’t agree with this part of your post because….” or “How did you get this in your post, it looks really cool….”

I’m sure these lovely people are tired of only getting comments from me! Not the point of the blog! SO check out the following peoples’ blogs: Cassandra, Duncan, Jack, Mason, Javiera, and Tyson.

This past week I asked all of you for various reflections, and offered the option of putting them on your blogs or into the checklist. As of this moment (Sunday morning), I have only seen reflections via the checklists, none via blogs. 🙁 So I’ll assume that most of you would prefer to do this anonymously, which is okay, I get that. But geez, I still want to share them with you all, they’re so good, so here they are, anonymously. I have just copy/pasted the words, no editing. Note that my words are in black font, and any different colour of font means a different person’s words:

TS5 students had to summarize about how to find the missing terms in a sequence, which was the slides that looked like this: 

1.Find your constant: divide the right term by left term (if there is no blank between them => this is your constant! if there is one blank => sqrt the answer and this is your constant, if there are 2 blanks => cuberoot the answer and this is your constant,etc)
2.Solve: multiply by the constant to find missing numbers.

It is basically just solving a pattern, like we did back in grade 7 and 8 with some extra stuff. If the sequence was in an increasing order you divide the large number into the previous smaller number. If they are in a decreasing order, you would divide the smaller number by the larger number to obtain the constant multiplier. If they were more than one number missing beside each other, you would still do the first step the same, but then you would have to find the x root of the number obtained, where x is the number of missing values in the sequence.

by doing trial and error and finding the pattern that was being used

if was easy

SN5 students were asked to write about equivalent exponential things, which was the slides that looked like this:

After looking at the answer, I felt like I was thinking too much about it, I was searching for super hard stuff that I wouldn’t understand when really, there wasn’t stuff I did not know or understand. So this activity helped me with english rules, and it refreshed my memory. (Funny how fast we can forget something over the break, luckily, it comes back as quickly when we get our head into it)

I learn that exponential functions can have A LOT of different shapes

well i learned that looks can be deceiving with dealing with exponents.

What I learned from this activity is that sometimes the equation of a function does not look similar at all to another one and it actually is if you simplify and turn it around. But I am having a lot of trouble with this part of the exponential function lesson :S

I learned that there are several ways of writing the same equation!

I learned that there are several ways of finding equivalent equations that I did not know about before and now I am using these techniques to do the work given to me 🙂

I learned a lot from this activity looking at the different equations that are the same on the graph! I think I need to make sure I know how to do everything without geogebra & then ill be good to go 🙂

Me again. Thank you to these writers, and I am hoping that more will come in later today, since everyone was supposed to have done this already. At any rate, when you look at this coming week’s checklist, you will notice that the first item is to reply to the above reflections, right here. I want your reactions – do you agree with what they’re saying? Do you have a question? Were these interesting or helpful to read?